Udacity_AB_Testing
Background
Udacity published a course for A/B Testing, also known as split tests, which are online experiments used to test potential improvements to a website or mobile app. Udacity’s AB Testing course is presented by Google and focuses on design and analysis of A/B tests. The course covers how to choose and characterize metrics to evaluate your experiments, how to design an experiment with enough statistical power and how to analyze the results and draw valid conclusions. This is the final project in the course.
I used the template provided by Udacity and provided my walk-through solution (highlighted in yellow) in each section with detailed python calculations stored in AB_Testing_Code.ipnyb. To view it with images and formulas properly rendered on GITHUB, please view via Github Pages.
For those who have never done A/B testing before, I recommend watching the Udacity A/B testing course, and if you still have time, read through the summary wonderfully done by others in the resource links below before attempting the final project on your own. For me, it was a stepping stone to know how to start the project as it opens up many possibilities on how to implement the test (ie. Python, or simple excel calculations, github etc). Initially, I created a rough draft on Evernote, compiling all my calculations solely based on the basic Windows calculator and Excel spreadsheet to be familiar with the analysis, then I write in Python to replicate the same results in vscode as a README (my first time!!!). Creating a git and using markdown template on vscode was a great learning experience for me as I wanted to share this as my first GITHUB project.
Resource links
- Udacity A/B Testing Project link
- Analysis done by Nikhil Sawal on towardsdatascience
- Analysis done by Andrew Bauman on GitHub
- Analysis done by Tammy Rotem on Kaggle
Final Project Instructions
Experiment Overview: Free Trial Screener
At the time of this experiment, Udacity courses currently have two options on the course overview page: “start free trial”, and “access course materials”. If the student clicks “start free trial”, they will be asked to enter their credit card information, and then they will be enrolled in a free trial for the paid version of the course. After 14 days, they will automatically be charged unless they cancel first. If the student clicks “access course materials”, they will be able to view the videos and take the quizzes for free, but they will not receive coaching support or a verified certificate, and they will not submit their final project for feedback.
In the experiment, Udacity tested a change where if the student clicked “start free trial”, they were asked how much time they had available to devote to the course. If the student indicated 5 or more hours per week, they would be taken through the checkout process as usual. If they indicated fewer than 5 hours per week, a message would appear indicating that Udacity courses usually require a greater time commitment for successful completion, and suggesting that the student might like to access the course materials for free. At this point, the student would have the option to continue enrolling in the free trial, or access the course materials for free instead. This screenshot shows what the experiment looks like.
<font color = red> The hypothesis was that this might set clearer expectations for students upfront, thus reducing the number of frustrated students who left the free trial because they didn’t have enough time—without significantly reducing the number of students to continue past the free trial and eventually complete the course. If this hypothesis held true, Udacity could improve the overall student experience and improve coaches’ capacity to support students who are likely to complete the course.</font>
The unit of diversion is a cookie, although if the student enrolls in the free trial, they are tracked by user-id from that point forward. The same user-id cannot enroll in the free trial twice. For users that do not enroll, their user-id is not tracked in the experiment, even if they were signed in when they visited the course overview page.
1. Metric Choice
Which of the following metrics would you choose to measure for this experiment and why? For each metric you choose, indicate whether you would use it as an invariant metric or an evaluation metric. The practical significance boundary for each metric, that is, the difference that would have to be observed before that was a meaningful change for the business, is given in parentheses. All practical significance boundaries are given as absolute changes.
Any place “unique cookies” are mentioned, the uniqueness is determined by day. (That is, the same cookie visiting on different days would be counted twice.) User-ids are automatically unique since the site does not allow the same user-id to enroll twice.
| Metrics | Definition |
|---|---|
| Number of cookies | Number of unique cookies to view the course overview page (dmin=3000) |
| Number of user-ids | Number of users who enroll in the free trial. (dmin=50) |
| Number of clicks | Number of unique cookies to click the “Start free trial” button (which happens before the free trial screener is trigger). (dmin=240) |
| Click-through-probability | Number of unique cookies to click the “Start free trial” button divided by number of unique cookies to view the course overview page. (dmin=0.01) |
| Gross conversion | Number of user-ids to complete checkout and enroll in the free trial divided by number of unique cookies to click the “Start free trial” button. (dmin=0.01) |
| Retention | Number of user-ids to remain enrolled past the 14-day boundary (and thus make at least one payment) divided by number of user-ids to complete checkout. (dmin=0.01) |
| Net conversion | Number of user-ids to remain enrolled past the 14-day boundary (and thus make at least one payment) divided by the number of unique cookies to click the “Start free trial” button. (dmin=0.0075) |
You should also decide now what results you will be looking for in order to launch the experiment. Would a change in any one of your evaluation metrics be sufficient? Would you want to see multiple metrics all move or not move at the same time in order to launch? This decision will inform your choices while designing the experiment.
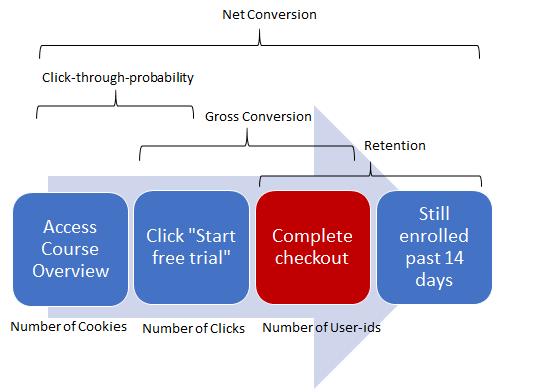
My understanding of this experiment:
The ultimate goal is to minimize student frustration and to most effectively use limited coaching resources. Setting clearer expectations upfront will reduce number
Experiment Hypothesis: Setting clearer expectactions upfront will reduce Gross Conversion but
Red box indicates point of change in the process flow in this test.
Invariant metrics: These metrics represent user activities before the user will experience the change, thus they are considered invariant.
- Number of cookies - This is the unit of diversion and even distribution would be expected between control and experiment groups, thus considered invariant.
- Number of clicks - Number of unique users to click on the free trial button would also expected to be evenly distributed between control and experiment groups since at this point in the funnel, the change has not occurred yet, thus considered invariant.
- Click-through-probability - This metric is entirely driven from the previous 2 metrics, and if both expected to be invariant, this is automatically considered invariant too.
Evaluation metrics: Metrics with the possibility of different distributions between experiment and control groups as a function of the experiment. Each evaluation metric is associated with a minimum difference (dmin) that must be observed for consideration in the decision to launch the experiment.
- Gross Conversion - If the hypothesis is true, Gross Conversion will decrease with less students starting the free trial (only those who would commit >5 hours per week would sign up)
- Retention - If the hypothesis is true, there will be an increase in Retention with more users staying beyond the free trial in the experiment group. (clearer expectation of commitment upfront will have less users quitting during free trial)
- Net Conversion - If the hypothesis is true, Net Conversion may not be significantly impacted. There may a slight increase with the rate of users staying beyond the free trial is slightly higher than the declining rate of Gross conversion.
Not selected as invariant / evaluation metric: Number of User IDs
User-ids are tracked only after enrolling in the free trial. The experiment may affect the number of users enrolling in the free trial, thus this metric is not invariant. It is not a good evaluation metric either as change in user IDs is not useful to prove that it may be due to the change in number of frustrated users. Number of user IDs may decline due to the decline in number of clicks. Equal distribution between the control and experiment groups would not be expected.
2. Measuring Variability
This Final Project Baseline Values spreadsheet contains rough estimates of the baseline values for these metrics (again, these numbers have been changed from Udacity’s true numbers).
For each metric you selected as an evaluation metric, estimate its standard deviation analytically. Do you expect the analytic estimates to be accurate? That is, for which metrics, if any, would you want to collect an empirical estimate of the variability if you had time?
Solution:
The analytical estimate of standard deviation tends to be near the empirically determined standard deviation for those cases in which the unit of diversion is equal to the unit of analysis.
This is the case for Gross Conversion and Net Conversion, but <font color = red> not Retention</font>. If we do ultimately decide to use Retention, then we should calculate the empirical variability.
Evaluation Metric Probability dmin SD Gross Conversion 0.206250 0.0100 0.0202 Retention 0.530000 0.0100 0.0549 Net_Conversion 0.109313 0.0075 0.0156
3. Sizing
3.1 Choosing Number of Samples given Power
Using the analytic estimates of variance, how many pageviews total (across both groups) would you need to collect to adequately power the experiment? Use an alpha of 0.05 and a beta of 0.2. Make sure you have enough power for each metric
3.2 Choosing Duration vs. Exposure
What percentage of Udacity’s traffic would you divert to this experiment (assuming there were no other experiments you wanted to run simultaneously)? Is the change risky enough that you wouldn’t want to run on all traffic?
Given the percentage you chose, how long would the experiment take to run, using the analytic estimates of variance? If the answer is longer than a few weeks, then this is unreasonably long, and you should reconsider an earlier decision.
Solution:
To calculate the sample size required for the experiment, the largest sample size required for one of the evaluation metrics will effectively be the size to go with. I plug in the following values into the online calculator for sample size:
- Baseline conversion rate: probability of each metric
- Minimum detectable effect: dmin of each metric
- beta: 0.2
- alpha: 0.05
Total pageviews required = Total unique cookies accessing course overview page
Gross Conversion probability:
Total cookies required in order to have 25835 clicks per group (control and experiment):Retention probability:
Total cookies required in order to have 39155 enrollments per group (control and experiment):Net Conversion probability:
Total cookies required in order to have 27413 clicks per group (control and experiment):
Evaluation Metric p dmin SD sample_size page_views Gross_Conversion (Enrollments/Clicks) 0.206250 0.0100 0.0202 25835 645875 Retention (Paid/Enrollments) 0.530000 0.0100 0.05495 39155 4746061 Net_Conversion(Paid/Clicks) 0.109313 0.0075 0.0156 27413 685325 Duration vs Exposure
4 million page views is significantly beyond the estimated 40K views we get on average daily. That would take us at least 100 days to collect the data, and typically any experiments taking longer than a few weeks is not reasonable, hence I decided to <font color=red>drop Retention</font> as a metric. <font color=blue>Net Conversion </font> has the largest number of page views of the remaining 2 evaluation metrics.
Duration at 100% exposure: 17 days
Duration at 75% exposure: 23 days
Duration at 50% exposure: 34 daysI decided to go with <font color=blue>75% exposure</font> since a 3 week duration to run the experiment is a reasonable length. 50% exposure rate with over a month long duration is not necessary as the risk is low since we do not expect a big drop in net conversion which may impact the company’s revenue. I personally try to avoid 100% exposure as I find that sometimes there are some business risks or technolgy issues resulting from running the experiment, and it is always good to hold back some traffic from the change.
There are similar analysis using different exposure rates than mine with good justifications as well, so definitely do your own reasoning to choose the right exposure.
4. Analysis
The data for you to analyze is in the data/ folder:
They contain the raw information needed to compute the above metrics, broken down day by day. (One for the experiment group, and one for the control group)
The meaning of each column: |Col header | Definition| |———–| ———-| |Pageviews | Number of unique cookies to view the course overview page that day.| |Clicks | Number of unique cookies to click the course overview page that day.| |Enrollments | Number of user-ids to enroll in the free trial that day.| |Payments | Number of user-ids who who enrolled on that day to remain enrolled for 14 days and thus make a payment. (Note that the date for this column is the start date, that is, the date of enrollment, rather than the date of the payment. The payment happened 14 days later. Because of this, the enrollments and payments are tracked for 14 fewer days than the other columns.) |
4.1 Sanity Checks
Start by checking whether your invariant metrics are equivalent between the two groups. If the invariant metric is a simple count that should be randomly split between the 2 groups, you can use a binomial test as demonstrated in Lesson 5. Otherwise, you will need to construct a confidence interval for a difference in proportions using a similar strategy as in Lesson 1, then check whether the difference between group values falls within that confidence level.
If your sanity checks fail, look at the day by day data and see if you can offer any insight into what is causing the problem.
Solution:
Before analyzing results from the experiment, sanity checks should be performed. These checks help to verify if the experiment was conducted as expected and that other factors did not influence the data which we collected. This also makes sure that data collection was correct.
Two of these metrics are simple counts like number of cookies or number of clicks and the third is a probability (CTP). We will use two different ways of checking whether these observed values are within expectations.1. Sanity Checks for differences between counts
I use binomial distribution (p = 0.5) to determine if the probability for Number of Cookies and Number of Clicks is within the margin of error at 95% confidence interval since the cookies are randomly assigned to either control or experiment group.
What we want to test is whether our observed fraction, 𝑝̂ (# of samples in control or experiment group divided by total # of samples in both groups) is not significantly different than p=0.5 . If the observed 𝑝̂ is within the margin of error range acceptable at a 95% confidence level, we passed the sanity checks! =)
Invariant Metrics Experiment Control SD MOE Lower_Bound Upper_Bound p_observed Pass_Sanity Number of Cookies 344660 345543 0.000602 0.001180 0.498820 0.501180 0.500640 TrueNumber of Clicks 28325 28378 0.002100 0.004116 0.495884 0.504116 0.500467 TrueObserved fraction is within bounds,<font color=green> passing sanity checks</font> for both metrics.
2. Sanity Checks for differences between probabilities (Click-through-probability)
We want to make sure the proportion of clicks given a pageview (our observed CTP) is about the same in both groups (since this was not expected to change due to the experiment).
In order to check this out we will calculate the CTP in each group and calculate a confidence interval for the expected difference between them.
In other words, we expect to see no difference ( CTPexp−CTPcont=0 ), with an acceptable margin of error, dictated by our calculated confidence interval. <font color=blue>The changes we should notice are for the calculation of the standard error, which in this case is a pooled standard error.</font>
Invariant Metric CTP_Experiment CTP_Control Ppool Diff_in_CTP SDpool MOEpool Lower_Bound Upper_Bound Pass_Sanity Click through Probability 0.0822 0.0821 0.0822 0.0001 0.0007 0.0014 0.0808 0.0836 TrueObserved fraction is within bounds,<font color=green> passing sanity checks</font> for Click-through-Probability metric.
4.2 Check for Practical and Statistical Significance
Next, for your evaluation metrics, calculate a confidence interval for the difference between the experiment and control groups, and check whether each metric is statistically and/or practically significance. A metric is statistically significant if the confidence interval does not include 0 (that is, you can be confident there was a change), and it is practically significant if the confidence interval does not include the practical significance boundary (that is, you can be confident there is a change that matters to the business.)
If you have chosen multiple evaluation metrics, you will need to decide whether to use the Bonferroni correction. When deciding, keep in mind the results you are looking for in order to launch the experiment. Will the fact that you have multiple metrics make those results more likely to occur by chance than the alpha level of 0.05?
Solution:
Based on the experiment results, we have 23 days of enrollment, so to calculate the probability of the evaluation metrics, the data points should be retrieved from those 23 days only.
The next step is looking at the changes between the control and experiment groups with regard to our evaluation metrics to make sure the difference is there, that it is statistically significant (difference is not due to chance) and most importantly practically significant (the difference is “big” enough to make the experimented change beneficial to the company).Practical Significance Test:
To determine the practical significance level, the probability of difference(Pdiff) between the control and experiment group has to be larger than dmin. Compute difference between Gross Conversion Experiment and Control group. Repeat the same for Net Conversion.
Statistical Significance Test:
Statistically significant means a result is unlikely due to chance. The p-value is the probability of obtaining the difference we saw from a sample (or a larger one) if there really isn’t a difference for all users.
Statistical significance doesn’t mean practical significance. Only by considering context can we determine whether a difference is practically significant; that is, whether it requires action.
It is statistically significant if:
- The confidence interval does not cross zero.
- The observed p difference is not small, within CI range.
- The observed p difference is less than alpha (A conventional (and arbitrary) threshold to indicate it is highly unlikely result occured by chance)
With large sample sizes, you’re virtually certain to see statistically significant results, in such situations it’s important to interpret the size of the difference.
Small sample sizes often do not yield statistical significance; when they do, the differences themselves tend also to be practically significant; that is, meaningful enough to warrant action.
Refer further details here: https://measuringu.com/statistically-significant/
Metrics Experiment Control Ppool dmin SDpool MOE Pdiff Lower Upper Gross_Conversion 0.198320 0.218875 0.208607 0.0100 0.004372 0.008569 -0.020555 -0.029124 -0.011986 Net_Conversion 0.112688 0.117562 0.115127 0.0075 0.003434 0.006731 -0.004874 -0.011604 0.001857
Based on the table calculations above:
<font color=green>Gross Conversion metric is practically significant</font> as the probability difference between experiment and control group, Pdiff is -2%, which is greater than the 1% dmin change.
It is also <font color=green>statistically significant</font> since Pdiff is -0.02, which is within the 95% confidence interval range: [-0.029124, -0.011986] and the CI does not include 0.<font color=red>Net Conversion metric is NOT practically significant</font> as the probability difference between experiment and control group, Pdiff is -0.4%, which is lower than the 0.75% dmin change.
It is also <font color=red>NOT statistically significant</font> since Pdiff is -0.004, which is a very small decrease and as such is not statistically significant. The 95% confidence interval range: [-0.011604, 0.001857] indicates the CI does include 0.
4c. Run Sign Tests
For each evaluation metric, do a sign test using the day-by-day breakdown. If the sign test does not agree with the confidence interval for the difference, see if you can figure out why.
Solution:
In a sign test, we check if the trend of change we observed (increase or decrease) was evident in the daily data.
Based on above results analysis, I expect to see experiment group with lower gross conversion rate and net conversion rate than the control group. Compute the Gross Conversion and Net Conversion daily per group, then count how many days each metric was lower in the experiment group and this will be the number of successes for the binomial test to calculate the two-tail P value.
I use an online binomial tool to calculate the two-tail P value. >You can implement the calculations behind it by referring to Tammy Rotem’s kaggle solution.
Gross Conversion comparison: 4 failures, 19 successes
So, P-Value of the test is 0.0026. Since the probability to pass the test daily is 1-0.0026 = 0.9974 which is greater than 95%, this result does not happen by chance (statistically significant) and <font color=green>it passes the sign test</font>.
Net Conversion comparison: 10 failures , 13 successes
So, P-Value of the test is 0.6776. Since the probability to pass the test daily is 1-0.6776 = 0.3224 which is lower than 95% , <font color=red>it does NOT pass the sign test.</font> The experiment will not have statistical significance impact on Net Conversion.
5. Summary
State whether you used the Bonferroni correction, and explain why or why not. If there are any discrepancies between the effect size hypothesis tests and the sign tests, describe the discrepancy and why you think it arose.
Solution:
This experiment diverts cookies into two groups, experiment and control randomly. The experiment group sees a screen triggering them in the free trial signup process to input the amount of time they are willing to commit to study, and the control group does not see the screen.
Three invariant metrics (Number of Cookies, Number of clicks on “start free trial”, and Click-Through-Probability) are chosen for purposes of validation and sanity checking. Gross Conversion (enrollment/cookie) and Net Conversion (payments/cookie) are identified as the evaluation metrics. The null hypothesis is that there is no difference in the evaluation metrics between the groups. In order to launch this experiment, the null hypothesis must be rejected for ALL evaluation metrics (statistically significant) and must meet or exceed the practical significance level for ALL evaluation metrics.
We expect Gross Conversion to decrease and Net Conversion to increase. Since we need both metrics to pass the test, the sign test is focus on finding any false negatives as false negatives have greatest impact when ALL metrics must be satisfied to trigger launch. Bonferroni correction method is not suitable as it is used for controlling type I errors (false positives) when using multiple metrics in which relevance of ANY of the metrics matches the hypothesis. The risk of type I errors increases as the number of metrics increases (significance by random chance).
Net Conversion is neither statistically nor practically significant in both the effect size test and sign test whereas Gross Conversion is statistically and practically significant for both tests.
6. Make a Recommendation
Finally, make a recommendation. Would you launch this experiment, not launch it, dig deeper, run a follow-up experiment, or is it a judgment call? If you would dig deeper, explain what area you would investigate. If you would run follow-up experiments, briefIy describe that experiment. If it is a judgment call, explain what factors would be relevant to the decision.
Solution:
Gross conversion is practically and statistically significant in this experiment, showing a decline in number of users signing up for free trial without any significant (statistically and practically) impact to the Net Conversion rate. This means the number of users remain enrolled after free trial which is the main source of revenue for the company is not affected by this experiment (neither increasing nor decreasing), indicating very low risk of financial losses. Considering that it did not impact the Net Conversion (no change in revenue, which means little benefits to implement the change), I would recommend to NOT launch this experiment, and run other experiments instead.
7. Follow-Up Experiment: How to Reduce Early Cancellations
If you wanted to reduce the number of frustrated students who cancel early in the course, what experiment would you try? Give a brief description of the change you would make, what your hypothesis would be about the effect of the change, what metrics you would want to measure, and what unit of diversion you would use. Include an explanation of each of your choices.
Solution:
(This is not a solution…but I think he did a pretty fantastic job here so I shall refrain from attempting to make up a crappy recommendation myself..) Feel free to check out Andrew Bauman’s analysis including follow up experiment suggestions. I am sure I missed out on other good examples on the web, so please feel free to share. I am always looking to learn and improve since this is my first A/B testing project. I will be more than happy to include here as reference for others too.
Retrospective
It took me about 15 days to complete this project with average 3-4 hours spent each day. I have never done an A/B testing project from start to finish but I have basic understanding of statistics and Python libraries like numpy and pandas. I was completely new to creating git and using vscode and markdown. I spent about 10 days going through course and creating the rough draft on Evernote. The other 5 days was spent on recreating the excel calculations in Jupyter noteboook using Python and writing explanations on both Jupyter notebook and formatting on README.
I love open source =)